Las escalas de categorías{1} son, con toda probabilidad, las escalas que se utilizan de forma más habitual para medir satisfacción, creencias, preferencias, actitudes,… y ello en muy diversos formatos y ámbitos: estudios de encuesta; cuestionarios referidos a constructos educativos, psicológicos o sociales; escalas de valoración en evaluaciones educativas, etc. Son escalas cómodas, que permiten la elaboración de instrumentos con respuestas claras y ordenadas, así como una recogida de datos cuantitativos fácilmente abarcable que no precisa de un número elevado de categorías. Entre las más comunes, dentro del entorno de las investigaciones educativas, se encuentran las escalas Likert, fácilmente entendibles por el entrevistado, y construidas, por lo común, con distintos cuantificadores lingüísticos, normalmente de cantidad (todo, algo, nada, etc.) o de frecuencia (siempre, a veces, nunca, etc.).
No cabe duda de que la versatilidad y comodidad de estas escalas facilitan a los profesionales de los ámbitos aplicados, no siempre acostumbrados a los tratamientos estadísticos, realizar sin grandes complicaciones recogidas de datos según los fines sustantivos de sus investigaciones. Sin embargo, las ventajas que aportan contrastan con el delicado análisis estadístico que posteriormente precisan sus medidas. No se trata de datos complejos desde el punto de vista métrico. Tampoco requieren tratamientos estadísticos más sofisticados que los de las escalas métricas continuas. El problema reside en que no hay criterios definitivos establecidos acerca de cuáles son las técnicas o modelos más adecuados, resultando que con frecuencia son analizadas mediante estrategias que exigen ciertos supuestos matemáticos que las escalas de categorías no cumplen.
En esta línea, algunos de los argumentos matemáticos que se establecen en ocasiones sobre ellas, no cuentan con la base suficiente. La cuestión relativa a los niveles de medida que alcanzan (como máximo ordinal) no permite asumir que, por el hecho de que sus categorías o cuantificadores estén ordenados, lo hagan con igual intensidad como si de una escala de intervalo se tratara, adquiriendo las propiedades métricas de ésta última. Los datos que aportan no pueden ser sumados o promediados, como es preciso realizar en cualquier modelo estadístico que exija supuestos (pruebas paramétricas, regresión lineal, análisis factorial, etc.). En palabras de Siegel (1988: 21), cuando las operaciones aritméticas se hacen con puntuaciones que no son verdaderamente numéricas, ocasionan deformaciones de los datos y menoscaban el valor de las conclusiones de la prueba. Es éste un argumento suficiente para poder considerarlas, dentro de su simplicidad y sencillez, escalas con métrica delicada, lo que justifica las sugerencias analíticas que exponemos en los siguientes apartados.
El objetivo de este trabajo se limita a comentar algunas herramientas estadísticas útiles para escalas categóricas (unas conocidas por los lectores acostumbrados a esta temática, y otras algo más novedosas y complejas). No se pretende, pues, mostrar un panorama completo de los posibles análisis necesarios, como tampoco realizar una exposición exhaustiva de cada uno de ellos. Planteamos de manera sencilla algunas sugerencias que consideramos de interés para el contexto de las evaluaciones educativas, en la idea de completar o sustituir algunas de las pruebas que se emplean habitualmente con estas escalas y que, desde el punto de vista matemático, no están suficientemente justificadas.
1. DESARROLLO
1.1. Un panorama confuso
A nuestro entender, son varias las razones que pueden explicar el tratamiento estadístico inadecuado que en no pocas ocasiones se aplica a las escalas de categorías. Hace unas décadas eran analizadas meramente con recuentos (frecuencias absolutas o relativas) de cada una de las categorías de respuesta, completando la información con simples polígonos de frecuencias o diagramas sectoriales. Sin duda el empleo de ordenadores y el desarrollo de software estadístico han aumentado exponencialmente el uso de modelos más sofisticados, manejando grandes cantidades de datos y variables. Las técnicas estadísticas utilizadas en las ciencias experimentales con un marcado carácter confirmatorio (las pruebas paramétricas de significación, el Modelo Lineal, o el Análisis Factorial, por ejemplo), aplicadas a variables continuas obtenidas con instrumentos precisos, fueron trasladadas directamente al análisis de escalas categóricas como si de una sencilla generalización se tratara. La facilidad para el usuario no especializado en el manejo de los programas informáticos ha contribuido también de manera notable.
Sin embargo, este mismo desarrollo de programas y herramientas ha ampliado la oferta con un considerable número de modelos estadísticos especialmente diseñados para trabajar con variables no métricas (discretas, ordinales o nominales), entre las que se encuentran las escalas de categorías. Si hablamos de modelos de dependencia, por ejemplo, encontramos la familia de Modelos Lineales Generalizados, el Análisis Discriminante o el Análisis de Correlación Canónica con variables ficticias, entre otros (siguiendo la clasificación de Hair, Anderson, Tatham y Black, 1999: 16-17). Si lo que se desea es descubrir patrones internos en los datos, contamos con modelos de interdependencia, como los Análisis de Conglomerados, Escalamiento, Componentes Principales no lineal, o Correspondencias, todos ellos con opciones no métricas.
En relación a los índices estadísticos que asocian las categorías de respuestas, bien por sujetos o bien por variables (ítems o reactivos), se ha abusado en exceso de la correlación producto momento de Pearson, un coeficiente que únicamente posibilita asociar variables métricas continuas linealmente relacionadas. Hace mucho tiempo que se conocen otros coeficientes no paramétricos (Kendall, Spearman, tetracórico,…), así como numerosas pruebas no paramétricas alternativas a los test paramétricos de significación (Mann-Whitney, Kruskall-Wallis, Friedman, etc.). Las pruebas paramétricas pueden emplearse siempre que las suposiciones que plantean acerca de la naturaleza de la población de la que se obtuvieron los puntajes sean acertadas, es decir, que el modelo en el que se basan represente el comportamiento de la variable en la población. Y, para que esto ocurra, las variables deben haberse medido al menos en una escala de intervalo, de manera que sea posible usar operaciones aritméticas con sus valores (Siegel, 1988: 21). Otro tanto puede decirse de las medidas de proximidad, entre las cuales la distancia euclídea es la opción más adecuada para las escalas Likert, por ejemplo.
En estas alternativas analíticas subyace un rasgo común que quizá haya contribuido también a la resistencia en su empleo con escalas categóricas. Efectivamente, las pruebas no paramétricas tienen una menor potencia que sus alternativas paramétricas, debiendo trabajar con muestras mayores para conseguir una potencia equiparable (Siegel, op. cit.: 40). Es éste un aspecto en el que deseamos detenernos al menos un momento. Desde la conocida llamada de atención de Cohen acerca de la pobre potencia estadística de muchas investigaciones (Cohen, 1962), momento a partir del cual se desarrollaron numerosos métodos para poder estimarla en pruebas paramétricas (Cohen, 1988), poco se ha avanzado en este sentido. Las opiniones de unos investigadores y otros han estado enfrentadas, llegando a considerar algunos que se ha producido un uso abusivo del análisis de la potencia (ver, por ejemplo, Hoening y Heisey, 2001; algunas razones del debate se abordan también en López-González, 2003). Por el contrario, el análisis de la potencia en pruebas no paramétricas no ha tenido un especial eco en la literatura especializada, exceptuando algunos trabajos, como los de Noether (1987) y Mumby (2002). Muestra de ello es la escasa oferta informática al respecto{2}. No obstante, persiste la creencia de que efectivamente la potencia es claramente inferior en el caso de las pruebas no paramétricas. También la versatilidad en el manejo de estas pruebas para trabajar las variables explicativas es considerablemente menor. No pueden realizarse, por ejemplo, contrastes no paramétricos con más de una variable de agrupamiento, lo que sí es posible con el ANOVA, ANCOVA y MANOVA. Esto limita la posibilidad de estudiar conjuntamente dos o más variables independientes como explicación de la varianza, así como observar con un mismo modelo los posibles efectos principales y efectos de interacción.
Por otro lado, los modelos de interdependencia adecuados para escalas de categorías (el Análisis de Conglomerados, el Escalamiento no métrico o el Análisis de Componentes Principales no lineal) no terminan de sustituir al Análisis Factorial lineal para variables métricas continuas (puede consultarse un estudio detallado en López-González, Pérez-Carbonell y Ramos, 2011). Los primeros aportan salidas gráficas interesantes, pero no proporcionan indicadores suficientes del elemento a analizar (bien sea el sujeto o el ítem), como sí lo hacen, por ejemplo, las puntuaciones factoriales que se obtienen en el Análisis Factorial, y que con tanta facilidad pueden emplearse en posteriores análisis.
Otra explicación de un tratamiento estadístico dudoso reside sencillamente en el desconocimiento, por parte de algunos evaluadores del ámbito de la educación, de numerosos modelos estadísticos que, sin embargo, sí son familiares en entornos experimentales. Así sucede, por ejemplo, con los Modelos Lineales Generalizados (ver López-González y Ruiz-Soler, 2011). Cuando se trabaja con actitudes, conductas, atributos, que en su dimensión latente son continuos, pero se miden de forma no métrica, los datos no se ajustan al Modelo Lineal General e incumplen los supuestos de linealidad y normalidad. En este sentido hay un hábito muy extendido en cuanto al uso de estrategias lineales no adecuadas que cuesta modificar. Así, es fácil encontrar regresiones lineales o ANOVA realizados con variables categóricas ordinales y, sin embargo, son más escasos los informes de evaluaciones educativas que usen análisis loglineal, logit, probit, regresiones ordinales o regresiones de Poisson.
También es cierto que la inercia ha llevado durante tiempo a usar unos programas estadísticos y no otros. Por ejemplo, SPSS (Statistical Package for the Social Sciences) ha sido, y probablemente sigue siéndolo, el software más utilizado en nuestro entorno pedagógico. Y así como este programa cuenta con diversas opciones analíticas a emplear con ficheros de sintaxis, los usuarios se han centrado en las rutinas más fácilmente accesibles desde el amable entorno de ventanas de Windows. Numerosas posibilidades analíticas internas en cada una de las técnicas estadísticas que el programa oferta han sido frecuentemente obviadas por una parte importante de los investigadores de nuestro ámbito, unas veces por desconocimiento, otras por la complejidad que entraña saber qué instrucción es la adecuada y cuál es su sintaxis. Excel es otro programa disponible para cualquier usuario pero no contiene una oferta estadística que pueda competir, ya que se trata fundamentalmente de una hoja de cálculo. No tiene implementadas pruebas no paramétricas, por ejemplo, y tampoco trabaja modelos multivariantes de interdependencia. Esto no sucede con SAS, un software estadístico realmente ambicioso, con una amplia variedad de análisis multivariantes de dependencia y de interdependencia, así como de análisis gráficos. En las evaluaciones educativas no ha tenido, sin embargo, un eco acorde con sus claras potencialidades. La lista podríamos hacerla extensiva a S-plus, Systat, Minitab, BMDP, GLIM, Statistica, Stat-graphics, ViSta, etc. En la actualidad, y según nuestro criterio, R es el software más completo. En palabras de Brian D. Ripley, del Departamento de Estadística de Oxford, R es un avanzado sistema de computación de estadística con gráficos de enorme calidad que se encuentra disponible gratuitamente para la mayoría de sistemas operativos (cit. en Ruiz-Soler y López-González, 2009). R trabaja gran parte de los modelos estadísticos adecuados para el análisis de escalas de categorías. Sin embargo, aun habiendo conocido una amplia difusión en estos últimos años, todavía resulta inusual dentro del contexto de las evaluaciones educativas. En revistas de educación en castellano, los artículos de López-González y Ruiz-Soler (2011) y López-González e Hidalgo (2010) son ejemplo del uso de algunos de los mencionados análisis con dicho programa.
Un último apunte específico en relación con las escalas Likert. En el artículo de Carifio y Perla (2007) se afirma con contundencia que durante seis décadas ha habido en ámbitos de medicina, salud, psicología y educación, un uso de estas escalas plagado de malentendidos, ideas falsas y errores conceptuales. Ello ha generado la difusión de una serie de leyendas urbanas erróneas acerca de las escalas Likert y sus propiedades que han producido un considerable perjuicio al desarrollo de la investigación en dichos campos. Los autores critican numerosos trabajos, en especial el de Jamieson (2004) y los citados en él, denunciando los trucos que sugieren sobre cómo solventar las limitaciones que caracterizan la métrica ordinal de las escalas Likert, entre otras. La raíz del problema la sitúan los autores en el desconocimiento y mala comprensión generalizados de los trabajos originales de Likert (Likert, 1932 y Likert y Hayes, 1957). Por ejemplo, una de las confusiones consiste en considerar que los términos escala y formato de respuesta son lo mismo, asociándose escala a un formato de respuesta de intervalo y trasfiriendo las propiedades métricas de las variables de intervalo a las escalas en general (incluso aunque sean ordinales, como las escalas Likert). Por el contrario, otra confusión reside en el hecho de creer que las escalas Likert, por tratarse de medidas ordinales, siempre deben ser analizadas mediante pruebas no paramétricas, a lo que habría que objetar que hay pruebas suficientemente robustas, como el test F de ANOVA, cuyos valores p serían válidos trabajando con escalas Likert en ciertas condiciones, según Glass, Peckham y Sanders (1972){3}. Carifio y Perla llegan incluso a afirmar: F is not made of glass (2007). El artículo termina presentando una lista de los diez errores “top” (Top Ten Myths) acerca de las escalas Likert, junto a los diez contra-argumentos (antídotos, según ellos) que los previenen.
Como consecuencia del confuso panorama, del que apenas hemos señalado unas pinceladas, concretamos en los siguientes apartados algunas sugerencias que permitan superar una parte de los inconvenientes señalados, mejorando de este modo el tratamiento estadístico de estas escalas. En la Tabla 1 recogemos algunas alternativas ya mencionadas junto con otras que pasamos a comentar a continuación. Entendemos que las sugerencias que desarrollamos tienen un triple interés: en primer lugar, una posible mejora de la métrica de las escalas; del mismo modo, la búsqueda de dimensiones internas dentro de los datos; y, finalmente, el estudio de las respuestas que se obtienen a partir de unas dimensiones establecidas con anterioridad. Respecto al primero, destacamos la ley de Zift, sin duda una muy interesante sugerencia para transformar las escalas categóricas de frecuencias, y casi absolutamente desconocida en nuestro ámbito. En el segundo, comentamos algunos desarrollos del Análisis Factorial. Por último, y de forma algo más extensa, planteamos un Análisis Conjunto referido a una situación concreta de evaluación educativa.
Tabla 1. Sugerencias para el análisis de escalas de categorías
TIPO |
PRUEBA O ANÁLISIS QUE SE SUGIERE |
EN SUSTITUCIÓN DE |
|
En torno a la métrica |
Revisar cuantificadores lingüísticos |
Escala ordinal |
|
Asociación |
Correlaciones no paramétricas
|
Correlación de Pearson |
|
Proximidad |
Distancia euclídea cuadrado |
Distancia euclídea |
|
Test de significación |
Pruebas no paramétricas
|
Pruebas paramétricas
|
|
MODELOS MULTIVARIANTES |
Modelos de dependencia |
Modelos Lineales Generalizados
|
Modelo Lineal General
|
LA CONFIGURACIÓN DIMENSIONAL SE ESTABLECE A PRIORI |
|||
|
|||
Modelos de |
LA CONFIGURACIÓN DIMENSIONAL ES CONSECUENCIA DEL ANÁLISIS |
||
|
Alternativas complementarias al AF tradicional o lineal |
||
LA CONFIGURACIÓN DIMENSIONAL ES CONSECUENCIA DEL ANÁLISIS |
|||
|
Alternativas sustitutivas al AF tradicional o lineal |
||
MODELOS BASADOS EN LA TRI |
|||
|
|||
1.2. Sugerencias en torno a la medida
Una línea de trabajo en torno a la medida de las escalas Likert consiste en proponer nuevos cuantificadores lingüísticos de las respuestas que lleguen a alcanzar el nivel de medida de intervalos. Con esta intención hay que destacar el trabajo específico con cuantificadores de frecuencia que llevaron a cabo Schreisheim y colaboradores durante más de dos décadas (cit. en Schriesheim y Castro, 1996). Un estudio complementario es el que aportan Cañadas y Sánchez-Bruño (1998), presentando un listado de cuantificadores consistentes que garantizan el buen uso de las pruebas paramétricas para su análisis. El procedimiento que siguen para establecer los nuevos cuantificadores es francamente sencillo. Dados los valores mínimo y máximo de la escala y el número de categorías a utilizar, los nuevos valores de referencia necesarios para conseguir una escala con distancias iguales entre los puntos se calcularían mediante la expresión:
![]()
Donde P es la categoría, Vmax y Vmin son los valores máximo y mínimo de la escala y NP es el número de categorías de la escala (Cañadas y Sánchez-Bruño, op. cit.). El estudio lo desarrollan con distintos listados de cuantificadores, variando también los puntos de las escalas.
Por otro lado, una opción muy interesante para transformar a una escala métrica categorías de respuesta de las que se tenga la frecuencia correspondiente, es la ley de Zipf (Ruiz-Soler, 2004). Esta ley surge precisamente en el campo de las Ciencias Humanas, donde el lingüista George Kingsley Zipf descubrió la interesante regularidad que se produce en los textos literarios respecto de las palabras (Zipf, 1949). Lo que enuncia la mencionada ley es que las palabras son empleadas de tal modo que permiten la tarea de la comunicación tan eficientemente como sea posible.
Zipf encontró que contabilizando la frecuencia de cada palabra en un texto y ordenando después las palabras según sus rangos de ocurrencia, se cumplía que el producto del rango (r) por la frecuencia (Fr) daba lugar a un valor más o menos constante (C), tal que:
![]()
En el caso que nos ocupa, la ley Zipf podría emplearse en variables de conteo para estimar el verdadero valor de una categoría de respuesta -o de un elemento u objeto- frente a un conjunto de ellos, o bien para determinar el posicionamiento de dicha respuesta en una escala métrica. En la ecuación anterior, conociendo el valor de C se podría calcular la verdadera posición r de un objeto dentro de su correspondiente población. Harían falta algunos pasos previos (Ruiz-Soler, 2004), tales como: (a) seleccionar una muestra de categorías u objetos de la población a analizar; (b) ajustar un modelo adecuado a la situación que se está midiendo, y (c) calcular el verdadero rango –r- de los objetos a partir del paso anterior.
Pongamos un ejemplo intuitivo. Supongamos que los entrevistados responden a un cuestionario de manera tal que deben elegir entre varios “objetos” (actividades académicas, metodologías didácticas, recursos educativos, etc.). Se procedería del siguiente modo:
- Calcular el número de ocurrencias (de elecciones) de cada objeto.
- Ordenar de forma decreciente los objetos según las frecuencias del punto anterior.
- Ajustar un modelo de regresión de Poisson (ya que se trata de una variable de recuento).
- Recalcular el posicionamiento de cada objeto a partir de la aplicación de la expresión:
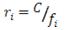
- Representar los pares de elementos para obtener la distribución poblacional.
- Encontrar el modelo que mejor se ajuste a los datos.
- Evaluar el modelo estimado, es decir, estimar si los datos cumplen la ley de Zipf a partir del valor del pseudocoeficiente de determinación (sería deseable un valor elevado, igual o mayor de 0.95).
- Calcular los nuevos rangos a partir de
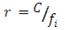 . Este paso tiene sentido desde el punto en que el rango calculado en el paso 4 no es el verdadero, sino una estimación muestral muy condicionada al número de objetos con el que se trabaja.
. Este paso tiene sentido desde el punto en que el rango calculado en el paso 4 no es el verdadero, sino una estimación muestral muy condicionada al número de objetos con el que se trabaja. - Posicionar los objetos gráficamente.
El resultado es una nueva ordenación de los objetos por medio de los rangos calculados, que ahora son métricos, indicando la distancia de cada uno de ellos respecto a aquel que resultó colocado inicialmente con el rango primero.
La utilidad de la ley de Zipf es considerable, permitiendo escalar incluso sujetos, lo cual cobra una especial relevancia en estudios de evaluación. Con posterioridad pueden estudiarse, por ejemplo, perfiles o tipologías de casos a partir de la ordenación obtenida, con la peculiaridad de que los valores ahora asignados a las categorías u objetos constituyen una variable continua, pudiendo ser analizados con pruebas adaptadas a escalas métricas.
1.3. Sugerencias en torno al análisis factorial
El Análisis Factorial (AF) es un modelo que pretende explicar la correlación entre un conjunto de variables observadas (las respuestas de los entrevistados a los ítems) y un pequeño conjunto de factores o dimensiones subyacentes no observables directamente. Este modelo ha tenido y tiene una importancia trascendental en la construcción de escalas para medir constructos (ver Yela, 1996). Una simple revisión de la literatura sobre elaboración de instrumentos permite constatar su presencia permanente en la exploración de factores o dimensiones teóricas de los instrumentos que se diseñan. Responde al interés del evaluador por encontrar una configuración interna en los datos, de modo que le sirva para explorar dimensiones con un planteamiento inductivo, o bien le confirme la estructura dimensional subyacente que debiera corresponder al diseño teórico que inspiró la escala en cuestión. No cabe duda de su utilidad. Ahora bien, no debe olvidarse que el Análisis Factorial tradicional o lineal (desarrollado en los inicios del estudio del modelo) requiere de ciertas condiciones que se ven afectadas por la escala de medida de las variables con las que se aplica. Los resultados sólo ofrecen confianza en el caso de que los datos sean verdaderamente continuos y multivariablemente normales, a fin de poder establecer relaciones lineales entre las variables originales, y entre éstas y los factores que se generan. Esto no es posible con las escalas de categorías, cuyo máximo nivel métrico es el ordinal.
Aun en el caso de que se utilice con variables métricas, son varios los problemas que frecuentemente se detectan:
- Gran trascendencia de las observaciones ausentes.
- Matriz de correlaciones inadecuada.
- Incumplimiento de los indicadores: determinante de la matriz de rotación oblicua; prueba de esfericidad de Barlett; prueba de adecuación muestral KMO; matrices de configuración y de estructura incoherentes.
- Incumplimiento del criterio de convergencia.
- Dificultad en la determinación del número exacto de factores.
A la lista anterior habría que añadir que, cuando el AF se emplea con variables no métricas, sucede en ocasiones que los indicadores cumplen los criterios exigidos, creando la ilusión de la conveniencia de la técnica, cuando en realidad se está forzando a que los datos encajen en el modelo olvidando las características matemáticas del mismo.
Sólo un par de comentarios al respecto. Desde el momento en que se detecta la presencia de observaciones ausentes -cuestión no atribuible a la naturaleza métrica de las variables- el análisis queda limitado al verse la muestra disminuida notablemente por tener que eliminar aquellos casos missing cuando se calcula la matriz de correlaciones. En segundo lugar, la matriz de entrada suele construirse muy frecuentemente con coeficientes de Pearson, incluso trabajando con items ordinales como si de variables linealmente relacionadas se tratara. Sin embargo, contamos de hecho con otros coeficientes no paramétricos mucho más adecuados, tal y como se ha indicado anteriormente.
Ante este panorama, la preocupación por el uso del Análisis Factorial con escalas categóricas no ha pasado desapercibida en la literatura especializada. El lector interesado puede consultar numerosos textos que ponen de manifiesto la heterogeneidad de los enfoques y valoraciones, entre los que destacan los de Bartholomew (2007: 17) y Bartholomew, Steele, Moustaki y Galbrain (2002: cap. 8). Baste decir, no obstante, que no hay una alternativa al Análisis Factorial tradicional que satisfaga suficientemente cuando se trata de trabajar con escalas categóricas. Quizá una de las razones resida en que las extensiones y generalizaciones del AF, en muchos casos, no han estado exentas de cierta complejidad matemática. De hecho, aunque el desarrollo inicial del AF correspondió a los psicólogos, en la segunda mitad del siglo XX fueron los estadísticos quienes avanzaron en los métodos computacionales asociados –Joreskog, 2007: 48-). Esto ha dificultado notablemente el conocimiento y comprensión de sus generalizaciones en los ámbitos aplicados, como es el caso de la evaluación educativa.
En definitiva, tres parecen ser las posturas adoptadas por los investigadores a la hora de valorar si el AF clásico es adecuado o no con escalas de categorías: (a) no hacer de ello un problema, siempre que se trate al menos de variables ordinales o discretas -como escalas Likert, por ejemplo-; (b) buscar alternativas analíticas para datos no métricos que complementen al AF clásico y que reduzcan también la información, empleándolas de forma conjunta, y (c) buscar alternativas que sustituyan al AF tradicional y que se adapten mejor a la métrica de las variables. Es en esta última donde se encuentran los desarrollos más complejos. Con el ánimo de clarificar, y aun a riesgo de un cierto simplismo, podríamos afirmar que dos parecen ser los caminos en esta tercera vía: encontrar el coeficiente de asociación más apropiado entre las variables de entrada y los factores que se generan, para realizar después un análisis basado en un modelo lineal (esto es, combinar el AF con un modelo de ecuaciones estructurales para datos categóricos), o bien plantear y ajustar un modelo de relaciones no lineales entre las variables observadas y el factor o dimensión común que se genera (aquí se encuentran los desarrollos del AF dentro de la Teoría de Respuesta al Item –TRI-).
Estas tres posturas generales de los investigadores respecto al tratamiento de las escalas de categorías con el AF, pueden sintetizarse en tres vías.
- Una primera vía, que siguen autores como como Nunnally y Bernstein (1995), quienes consideran la métrica de las escalas categóricas efectivamente más limitada que la de las variables continuas, pero más bien a nivel teórico, pudiendo ser tratadas como escalas continuas porque las distorsiones, según ellos, son mínimas. Una de las garantías es justamente el empleo de la matriz de correlaciones producto-momento de entrada, que estrictamente hablando es la única que puede usarse en el modelo. Según esta postura, las correlaciones y/o los componentes de la varianza no requieren una escala de razón y tampoco se ven afectadas por las desviaciones monótonas de cualquier escala de intervalo. Más aún: los métodos estadísticos son ciegos por completo a cualquier significado de los números implicados en el mundo real (Nunnally y Bernstein, 1995: 27).
- Una segunda vía, en la que se localizan modelos que comparten con el Análisis Factorial la intención de reducir las variables originales, pudiendo ser utilizados de forma complementaria y ayudando notablemente en la interpretación de la configuración dimensional. Se trata de modelos multivariantes de interdependencia, como el Análisis de Conglomerados, el Escalamiento Multidimensional no métrico con el algoritmo SMACOF y el Análisis de Componentes Principales no lineal o categórico. En esta línea y en el entorno de una evaluación educativa, un estudio comparado de los dos primeros con el Análisis Factorial puede consultarse en López-González et al. (2011). El Escalamiento Multidimensional no métrico se aborda en López-González e Hidalgo (2010), donde se sugiere emplearlo con el algoritmo SMACOF, a diferencia de lo que suele ser más común, que es el uso del algoritmo ALSCAL. En este trabajo se justifican las diferencias y ventajas entre una estrategia y otra, con una referencia especial a un estudio educativo. Un ejemplo del Análisis de Componentes Principales Categórico en una evaluación educativa lo encontramos en el artículo de Suárez y Jornet (2011). En todos estos trabajos se analizan escalas de categorías y se emplean alternativas mucho más adaptadas a la métrica, resultando que el ajuste del modelo a los datos mejora notablemente y la solución de las dimensiones internas resulta en cada caso más parsimoniosa y coherente con la concepción sustantiva que inspiró la escala. Todas ellas pueden ejecutarse con el programa R.
- Una tercera vía trabaja con opciones más avanzadas que, indudablemente, requieren procedimientos de estimación más complejos. Por ejemplo, el AF con un Modelo de Ecuación Estructural se desarrolla bajo el supuesto de la existencia de una variable de respuesta continua, que a su vez subyace a la respuesta ordinal observada en el ítem. Esto es, una variable “latente” de respuesta por cada cuantificador o categoría. De esta forma, las puntuaciones observadas pueden considerarse discretizaciones de continuos de respuesta normalmente distribuidos. Si esto es así, deberá buscarse una metodología de análisis que permita recuperar la “verdadera” estructura factorial que existe entre las variables latentes continuas. El índice de asociación apropiado en este caso será el estimador del coeficiente producto-momento a partir de variables discretizadas, o sea, la correlación policórica, para varias categorías, o tetracórica, en el caso de categorías dicotómicas. En esta línea un desarrollo específico para escalas de categorías se encuentra en Muthén (1984) y Muthén y Kaplan (1992). El ajuste se realiza por medio de mínimos cuadrados generalizados para escalas dicotómicas, o por máxima verosimilitud y mínimos cuadrados ponderados para escalas politómicas u ordinales (Flora y Curran, 2004).
Otro grupo de análisis avanzados en torno al AF son las extensiones relacionadas con la Teoría de Respuesta al Item. Básicamente consisten en ajustar un modelo de relaciones no lineales entre las variables observadas y el factor común, por ejemplo un modelo en el que dichas relaciones adopten la forma de la ogiva normal. En este grupo se encuentran el Análisis Factorial no lineal y el Análisis Factorial de Información Completa. El primero se debe a McDonald (1967), quien se opone a cualquier justificación posible del AF lineal con datos no continuos. El principio básico del AF no lineal es el mismo del AF lineal: las covarianzas residuales se anulan tras extraer el número apropiado de factores o dimensiones. Sin embargo, este modelo ajusta las regresiones entre el ítem y el factor mediante mínimos cuadrados, si bien con un polinomio cúbico, por lo que es de esperar que en la evaluación dimensional no aparezcan factores espurios debidos a la no linealidad. Desde un punto de vista teórico, este análisis, en palabras de Ferrando y Lorenzo (1994), parece ser la solución más limpia y elegante al problema de la falta de linealidad. Sin embargo, desde un punto de vista aplicado cabe considerar si el ajuste proporcionado compensa la notable complicación que se introduce en los procedimientos de estimación. Es esta misma línea Gaviria (1990) comenta la dificultad de comprender en las salidas el significado de algunos términos complejos, como los términos cuadráticos, cúbicos, cuádricos, etc., donde suelen reflejarse curvaturas, interacciones y otros fenómenos complejos, máxime teniendo en cuanta la facilidad con que los usuarios interpretan sus investigaciones cuando emplean el AF clásico.
El AF de Información Completa es especialmente interesante por el tipo de información de entrada que emplea. En el AF tradicional se utiliza la matriz de correlaciones entre los ítems de la escala, lo cual, como ya hemos comentado, tiene sus inconvenientes. El AF de Información Completa es una técnica diseñada de forma específica para aprovechar toda la información disponible, trabajando directamente con las frecuencias de los patrones de respuesta de los sujetos a los ítems, pero incorporando además la información que proviene de los parámetros de la TRI para estimar las cargas factoriales (por ejemplo, la adivinación por azar, la dificultad de los ítems, etc). Los referentes más destacados de este enfoque son los trabajos de Bock, Gibbons y Mulaki (1988) para escalas de categorías dicotómicas y Mulaki y Carlson (1995) y Swygert, McLeod y Thissen (2001) para escalas politómicas. En el ámbito educativo puede consultarse el artículo de López-González et al. (2011), donde se argumentan sus ventajas respecto a otras alternativas del AF, así como el trabajo de Joaristi y Lizasoain (2008), donde se presenta aplicado a una evaluación educativa.
La oferta informática para estos desarrollos no es amplia. Aunque las diversas extensiones del AF han ido publicándose en revistas especializadas, tal y como hemos ido viendo, los autores de los programas estadísticos más populares no han considerado conveniente incluirlos. Han sido investigadores a nivel particular quienes se han ocupado por desarrollar programas específicos que recojan estas alternativas. En España destacamos el programa FACTOR (Lorenzo y Ferrando, 2006), que permite trabajar con correlaciones policóricas. El AF no lineal se realiza con el programa NOHARM (Fraser y McDonald, 1988) y el AF de Información Completa se aplica con el programa TESTFACT (Bock, et al., 2003). El software R también va incorporando algunas de estas alternativas. Así, por ejemplo, el paquete Psych permite construir correlaciones policóricas y tetracóricas, y con irtProb puede realizarse un Análisis Factorial no lineal.
1.4. Análisis conjunto
Consideramos el Análisis Conjunto (AC) una técnica estadística con una gran potencialidad en el ámbito de la investigación educativa. Aun siendo poco conocida en este entorno es, sin embargo, un modelo multivariante ampliamente utilizado en otros campos, como en estudios de mercados y en estrategias de marketing. Comienza a implementarse a comienzos de los años setenta a partir del trabajo de Green y Rao (1971), extendiéndose con rapidez a múltiples ámbitos: situaciones del mundo de los negocios y de la administración pública, estudios en agricultura, economía de la salud, energía, economía ambiental, etc. En disciplinas más próximas al análisis de la conducta se aplica, por ejemplo, a los Modelos de Conducta Multiatributo (Fishbein y Aizen, 1975 y Aizen y Fishbein, 1980), frecuentemente utilizados en Psicología Comercial (Varela, Rial y García-Carreira, 2003: 511){4}. La generalización de este uso ha hecho que la oferta informática sea amplia, pudiendo ejecutarse mediante los programas SPSS, SAS y R. Por otra parte, su notable flexibilidad le ha permitido ser aplicado a casi cualquier entorno en el que sea relevante algún proceso de toma de decisiones o el desarrollo de estrategias a partir de dichas decisiones. Tal es el caso de las evaluaciones educativas, donde además son frecuentes las mediciones no métricas.
Dicha potencialidad y flexibilidad son evidenciadas a través de la doble función que el AC desempeña en la práctica: es un modelo estadístico que evalúa las preferencias en la elección de una idea, servicio o producto, y es a la par un método de investigación que incluye una serie de etapas propias de un diseño experimental. Todo ello hace del AC un modelo multivariante flexible, rico y con múltiples posibilidades de aplicación.
Su objetivo es valorar de manera realista las elecciones de los encuestados con relación a las diferentes características o atributos que tenga un determinado producto, idea, proyecto o servicio (real o hipotético). El fin último consiste en comprender las respuestas de los entrevistados y sus evaluaciones acerca de las posibles combinaciones predeterminadas de los atributos que potencialmente posean ese producto, idea u objeto. Es decir, cómo el encuestado desarrolla preferencias por una idea u otra, basándose en la premisa de que evalúa su valor global, pero combinando cantidades parciales del valor que él asigna a cada atributo. Esto se relaciona con los Modelos de Conducta Multiatributo, en el sentido de que las preferencias no se realizan por una percepción global de los atributos, sino a partir de una percepción evaluativa de los mismos. Por lo tanto, el AC permite explorar, incluso cuantificar, el sistema de valores de los sujetos en el momento de elegir una alternativa entre las posibles combinaciones multiatributos, así como conocer la importancia de cada uno de los valores en la decisión global de preferencia. En este sentido, al trabajar con una lógica similar a la de un diseño experimental, permite incluso utilizar un ajuste de modelos lineales con variables ordinales.
La utilidad, que es el concepto básico para medir el valor en el AC, es un juicio subjetivo de preferencia único para cada sujeto. La utilidad se supone basada en el valor asignado a cada uno de los niveles de los atributos y se expresa mediante una relación que refleja la forma en que se combinan dichos atributos. Otros términos asociados son el factor, que se emplea para describir un atributo específico y que hace la función de variable independiente, y los niveles que conforman cada factor. En términos generales, se trata de describir un objeto o idea respecto a su nivel en el conjunto de factores que lo caracterizan. Cuando un investigador selecciona los factores y los niveles que considera describen el objeto de acuerdo a un modelo teórico, esa combinación se conoce con los términos de tratamiento, estímulo o perfil. Al construir combinaciones específicas (estímulos), el evaluador llega a entender la estructura de preferencias del encuestado. Esa estructura de preferencias explica, además de la importancia de cada factor en la decisión global (en la elección), cómo los diferentes niveles de un factor influyen en la formación de una preferencia conjunta o utilidad.
Aun a riesgo de pecar de un cierto reduccionismo, pero prevaleciendo nuestro interés por presentar -siquiera de forma esquemática- ciertas alternativas para el análisis de escalas de categorías, nos parece interesante destacar dos diferencias y un rasgo común entre el Análisis Conjunto y el Análisis Factorial. Como ha quedado dicho, el AF es un modelo que se aplica, bien a las respuestas de los entrevistados para explorar estructuras internas (factores y dimensiones), o bien para confirmar una configuración previa entre ellos. En este sentido, su cometido es analizar las relaciones entre las respuestas observadas de los encuestados con los ítems de una escala, y entre éstas y los factores subyacentes. Como resultado, la configuración dimensional interna que aporta el AF a partir de los datos es teórica y producto del análisis. Por el contrario, el AC analiza las respuestas dadas por los entrevistados a un conjunto de estímulos reales, configurados previamente por el investigador en base a la información sustantiva que se tenga del objeto o idea, o en base a sus intereses particulares. Esa configuración es presentada al usuario en forma de estímulos o perfiles (de ahí su aproximación a un diseño experimental), frente a la cual la variable que se obtiene no es sin más una respuesta, sino una preferencia o valoración. El lector puede hacerse una idea de las potencialidades que encierra la creación de perfiles, combinando atributos y niveles dentro de los propios atributos. En definitiva, ambos modelos tienen en común trabajar con una configuración de dimensiones o factores, pero mientras que en el AF la configuración dimensional es teórica y se obtiene a posteriori como consecuencia del análisis, en el AC la configuración de dimensiones es real (en el sentido de estar generada a partir de ciertas características del ámbito empírico) y a priori, adquiriendo una función estimular.
Una segunda diferencia entre ambas técnicas es el tipo de modelo y los supuestos que requieren. El AF es un modelo de interdependencia en el que no median relaciones de dependencia entre las variables, siendo analizadas todas ellas de forma simultánea. Por contraste, el AC es un modelo de dependencia, actuando la utilidad como variable dependiente y los factores como las supuestas variables independientes. Desde el punto de vista métrico, el AC admite variables dependientes métricas y no métricas, variables predictoras categóricas, así como unos supuestos estadísticos acerca de las relaciones entre ambos tipos de variables mucho menos restrictivos (no es necesaria la linealidad del AF clásico, por ejemplo, ni la normalidad, homoscedasticidad e independencia de otros modelos de dependencia, como en el caso de las pruebas paramétricas). Por contra, los supuestos conceptuales en el AC son mucho mayores. Con anterioridad a la investigación el evaluador ha de especificar de forma general el modelo y debe diseñar consecuentemente la evaluación posterior, lo que hace imposible contrastar modelos alternativos una vez tomadas dichas decisiones. Como señalan Hair et al. (1999), el AC está muy determinado por la teoría en su diseño, estimación e interpretación (p. 433) y, por tanto, la concepción previa que guía la evaluación determina absolutamente su éxito posterior.
1.5. Sugerencias en torno a la evaluación de la cohesión social
Pongamos un ejemplo intuitivo tomando como referente la idea que plantea Jornet (2010) sobre la necesidad de promover la Cohesión Social (CS) como elemento guía de las políticas sociales, en particular de las políticas educativas como parte integrante de las primeras. En dicho trabajo se reflexiona acerca de la vinculación de la CS con elementos socio-económicos específicamente relacionados con el bienestar social, así como con los procesos de integración social. Como argumenta el autor, a partir de la definición de Cohesión Social que plantea el Consejo de Europa{5} se han aunado esfuerzos en aras de establecer diversas concreciones en la evaluación de los logros de la CS, definiéndose algunas tipologías de indicadores, como el Portafolios de Laeken (2006) -claramente insuficiente- o la Guía Metodológica del Consejo de Europa (2005) -algo más explícita- (cits. en Jornet, op. cit.) Ambas propuestas no constituyen en sí mismas un modelo, de hecho ni tan siquiera hacen referencia a un posible enfoque de acción educativa que esté conformado para promover la Cohesión Social. Como consecuencia, se plantea la necesidad de diseñar y desarrollar un modelo sistémico de evaluación, acreditación de instituciones y evaluación de la docencia que imparte el profesorado, que atienda de forma coherente los tres planos posibles de análisis: (a) evaluación de sistemas; (b) evaluación de instituciones, y (c) evaluación de la docencia universitaria. La tarea requiere reflexionar de forma previa y precisa sobre la configuración de los elementos a tener en cuenta en ese modelo, conectando todos los planos de intervención educativa, y buscando un nivel razonable de coherencia entre ellos, lo que aboca a un problema esencialmente complejo y multidimensional, instado por una pregunta fundamental: ¿podemos hacer algo desde la Educación para promover la Cohesión Social?
En relación a lo expuesto y en consonancia también con la definición de Cohesión Social, Jornet señala la conveniencia de medir adecuadamente el valor que la sociedad (personas y grupos) da a la educación (valor social de la educación) y relacionarlo posteriormente con los indicadores del bienestar social. Se trataría de detectar qué elementos comunes ofrecen a los ciudadanos un marco de Cohesión Social. No hay duda de que dichos elementos tendrían que extraerse de un macro-estudio, pero cabe pensar que el profesorado también puede vivirlos de forma parecida en la cotidianidad que le plantean sus relaciones con el alumnado y sus familias.
La dificultad para abordar un modelo de estas características en los tres planos señalados reside en identificar los CONSTRUCTOS que den respuesta a la mejora real de la Cohesión Social (Figura 1, pto. 1), de manera tal que queden atendidos los intereses de las AUDIENCIAS implicadas en cada plano. El hecho es que, tal y como apunta Jornet (2010), existe una gran desconexión entre las necesidades de información que se tienen para guiar la mejora en las aulas y las informaciones que provienen de evaluaciones externas. En este sentido lo ideal sería conectar los distintos NIVELES de análisis (sistema, instituciones, aulas) por medio de una coherente y ajustada identificación de las DIMENSIONES y constructos que puedan ser consideradas a través de todos ellos (Figura 1, pto. 2). Y así, más que buscar un modelo de evaluación global, habría que apostar por un diseño de modelos homogéneos para cada uno de los PLANOS, pudiendo trabajar con dos posibles ORIENTACIONES: inicialmente desde lo micro-analítico (la docencia en el aula), para terminar alcanzando en otro momento lo macro-analítico (la calidad del sistema) (Figura 1, ptos. 3 y 4).
Figura 1. Aproximación a un modelo de evaluación de la educación desde la cohesión social centrado en el aula
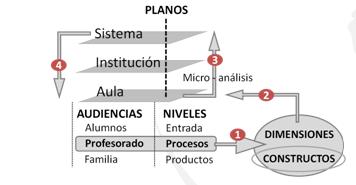
Tomando como punto de partida una orientación micro analítica, Jornet realiza una aproximación a un diseño de evaluación de la docencia en el aula dentro de una perspectiva de evaluación de la educación como promotora de la Cohesión Social. Un modelo más general de evaluación de la docencia tendría que contemplar los niveles de análisis de entrada/contextos, procesos y productos, pero su propuesta se centra por ahora en los elementos de proceso para las audiencias de alumnos, profesorado y familias. Lo peculiar es que las dimensiones tratadas terminarán estableciéndose también como elemento de verticalidad entre los planos mencionados: aula, escuela y sistema (Figura 1, ptos. 3 y 4). En la Tabla 2 mostramos las dimensiones y constructos a tener en cuenta en lo que respecta a la audiencia del profesorado.
Tabla 2. Dimensiones de evaluación de la docencia en el aula desde la perspectiva de la cohesión social. Audiencia: profesorado (Elaboración a partir de Jornet, 2010)
| DIMENSIONES DE DEFINICIÓN DE LA CS |
CONSTRUCTOS |
|
|
A1 |
Clima social en el aula |
A2 |
Gestión social del aula |
|
A3 |
Gestión de conflictos en el aula |
|
|
B1 |
Aprender a aprender |
B2 |
Resiliencia |
|
B3 |
Valor social de la educación |
|
B4 |
Competencia y desarrollo emocional |
|
|
C1 |
Metodología didáctica |
C2 |
Metodología de evaluación |
|
|
D1 |
Respeto, dignidad y reconocimiento |
D2 |
Inclusión: atención a la diversidad |
|
|
E1 |
Colaboración Familia-Profesorado |
E2 |
Estilos educativos familiares |
|
E3 |
Estilos educativos docentes |
|
La idea explicada en las líneas anteriores da pie a utilizar distintos modelos estadísticos para el análisis de los posibles datos a obtener. Estos comentarios van a establecerse a nivel intuitivo con el interés único de ser útiles para ejemplificar los modelos estadísticos que hemos sugerido en los anteriores apartados.
- Evaluación de la propuesta de constructos/dimensiones:
- A partir de la idea de Jornet sobre constructos y dimensiones de los elementos de proceso a evaluar, podría hacerse un Análisis Conjunto para cada una de las audiencias, trabajando en cada caso con la estructura particular de dimensiones y constructos respectivos. El objetivo sería determinar la importancia relativa que tienen las distintas dimensiones para la audiencia correspondiente (Figura 1, pto. 1).
- Los valores de preferencia que se obtengan en los Análisis Conjuntos permitirían analizar las funciones de valoración de los sujetos, así como sus preferencias por dimensiones y constructos. Pueden establecerse diferencias a partir de ciertas variables de clasificación, como centro, ciudad, comunidad autónoma, género, etc., empleando las correspondientes pruebas no paramétricas. Por otro lado, dependiendo de cómo se recojan las respuestas de los entrevistados (más adelante lo comentamos) se obtendrían escalas Likert por audiencias, permitiendo posteriores Análisis Factoriales (así como otros modelos de interdependencia complementarios –recordar la Tabla 1-). También puede recogerse el “perfil de mayor elección” registrando las frecuencias de los perfiles que, aplicando la ley de Zift, pueden después transformarse en escalas métricas. Obtenidas estas medidas, los posibles contrastes de significación se realizarían con pruebas paramétricas o con el Modelo Lineal General.
- Medición de constructos (elaboración de escalas):
- La medición de constructos habría de realizarse con instrumentos que tuvieran la calidad suficiente para garantizar los máximos niveles de validez y fiabilidad. Con relación a ello, es muy destacable el trabajo desarrollado en los Proyectos AVACO y MAVACO sobre elaboración de cuestionarios de contexto{6}. Muchos de estos instrumentos aportan escalas Likert con las que podrían emplearse Análisis Factoriales con un Modelo de Ecuación Estructural para datos categóricos, o cualquiera de las alternativas de AF basadas en la Teoría de Respuesta al Item. El resultado serviría para valorar la estructura de factores interna de cada constructo.
- Podrían analizarse además diferencias según variables de clasificación con pruebas no paramétricas, así como estudiar las posibles asociaciones entre constructos mediante coeficientes de correlación no paramétricos.
- Conexión entre niveles (entrada/procesos/productos):
- No cabe duda de que un análisis entre los niveles de entrada/proceso/producto aboca al establecimiento de modelos de dependencia donde se analizara la respuesta (producto) a partir de dimensiones y constructos explicativos de entrada y de proceso. Un producto habitual es la medida del rendimiento, que puede registrarse con variables métricas (pruebas de conocimiento), o no métricas (p.e. número de suspensos). El primer caso admite análisis con el Modelo Lineal General (regresión clásica, ANOVA, ANCOVA…); para el segundo se requieren Modelos Lineales Generalizados (ver Tabla 1). Cabría igualmente explorar una estructura de relaciones no lineales entre variables explicativas (de entrada y de proceso) y variables de respuesta (productos), lo que aconsejaría usar modelos aditivos{7}.
- Conexión entre planos (aula, institución, sistema):
- Alguna estrategia estadística que permita contemplar a un tiempo medidas de los tres planos necesariamente obliga a pensar en un análisis jerárquico. Un modelo lineal jerárquico permitiría simultanear el estudio en los planos de la estructura jerárquica de la Figura 1, tomando en cuenta los constructos de las correspondientes dimensiones en cada plano. Existen diversas alternativas de modelos jerárquicos con variables de respuesta métricas y no métricas que pueden consultarse en Raudenbush y Bryk (2002: cap. 10).
Antes de seguir adelante conviene hacer una pequeña aclaración. Sin duda el lector será consciente de las numerosas decisiones que conllevan las sugerencias analíticas que hemos comentado en este ejemplo. Debemos advertir que por encima de cualquier consideración estadística, a la hora de elegir una estrategia u otra priman los objetivos sustantivos de la evaluación. No podemos olvidar que todo aparato estadístico responde a los fines de la investigación en la que se desarrolla. Por ello, la configuración previa de las dimensiones adecuadas en cada plano, por ejemplo, o la determinación de los constructos correspondientes a cada dimensión, es una cuestión teórica que no determina el análisis. En todo caso, éste le ayuda al investigador a orientar sus decisiones.
1.5.1. Aproximación a un Análisis Conjunto
Comentamos a continuación cómo se plantearía un Análisis Conjunto tal y como ha quedado señalado en el apartado (a) anterior. Nos centramos en el plano del aula y en la audiencia del profesorado. El objetivo sería obtener una función que recoja la utilidad (el valor) que le reporta a cada profesor la Cohesión Social expresada a partir de la valoración que alcanzan las dimensiones que la definen. Lo ideal es trabajar con un número reducido de dimensiones y con pocos constructos en cada una de ellas. Por eso, si existen argumentos sustantivos que avalen una decisión previa para seleccionar unos y no otros, éste sería el momento de considerarlos.
Tabla 3. Diseño Ortogonal Para Elaboración De Perfiles En Un Análisis Conjunto De Evaluación De La Cohesión Social Desde Una Perspectiva Educativa
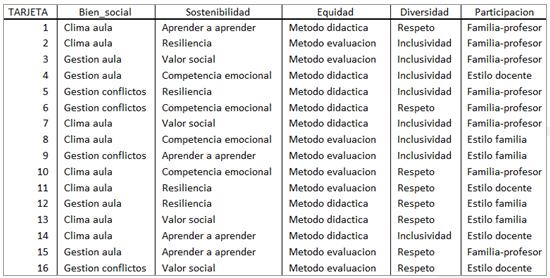
Si el diseño se realiza de forma completa (diseño de perfil completo) sería preciso trabajar las cinco dimensiones, consideradas ahora como atributos, siendo los niveles los constructos definidos en cada dimensión. La cantidad de combinaciones equivaldría a los posibles perfiles a evaluar: 3 X 4 X 2 X 2 X 3 = 144. Cada perfil describe una concepción completa y consta de una combinación diferente de niveles de factores para todos los atributos. No sería necesario evaluarlos todos. Podría elegirse aleatoriamente una muestra de perfiles por medio de un diseño ortogonal (diseño factorial fraccional) que asegure que todos los atributos o niveles figuren con idéntica intensidad en los perfiles presentados. Igualmente habría que balancear el orden de presentación de las dimensiones en el conjunto de perfiles. El resultado es un subconjunto representativo de perfiles (configurado ahora en tarjetas) diseñado para recoger los efectos principales de cada constructo. Se supone que las interacciones entre los niveles de un factor con los niveles de otro factor carecen de significado.
Por lo común las variaciones de las preferencias intra-sujetos suelen ser elevadas, por tanto, la mayor parte del AC se centraría en el caso único (cada profesor). Por el contrario, si interesara generalizar los resultados, se trabajaría con una muestra de profesores seleccionada con los criterios habituales de muestras representativas, debiendo ser su tamaño lo suficientemente grande para garantizar la fiabilidad{8}.
Seguidamente, a cada profesor de la muestra se le proporcionarían el conjunto de tarjetas y se registrarían sus respuestas. Las posibilidades de medida de las respuestas de los profesores serían varias: (a) que asignen una puntuación de preferencia a cada perfil empleando, por ejemplo, una escala Likert; (b) que anoten un número del uno al cien para indicar la preferencia, o (c) que ordenen los perfiles según la preferencia asignándoles un rango a cada uno, desde uno hasta el número total de perfiles.
A partir de este punto se ejecutaría el AC obteniéndose como resultado las puntuaciones de utilidad para cada constructo de la dimensión (contribuciones parciales). Dichas puntuaciones se interpretarían como coeficientes de regresión, en cuanto a que proporcionan una medida cuantitativa de la preferencia para cada constructo de la dimensión. Los valores mayores corresponden a una preferencia mayor. Además, pueden compararse porque se expresan en una unidad común, lo que permite considerarlas conjuntamente para obtener la utilidad total, es decir, la preferencia global de cualquier combinación de constructos de las dimensiones. En definitiva, las contribuciones parciales se constituirían en un modelo para pronosticar la preferencia de cualquier perfil, incluidos aquellos que no fueron presentados realmente a los profesores. Tal es la verdadera potencialidad del AC: la posibilidad de predecir la preferencia de perfiles que no han sido evaluados por los encuestados.
2. CONCLUSIONES
En este artículo hemos aportado algunas sugerencias para el análisis estadístico de escalas de categorías, con la intención de efectuar un tratamiento más sensible y acorde con la métrica que las caracteriza (discreta, ordinal, nominal). Tal y como señalamos, las escalas de categorías no son datos complejos desde el punto de vista métrico. Tampoco requieren tratamientos estadísticos más sofisticados que los de las escalas métricas continuas. El problema reside en que no hay criterios definitivos establecidos acerca de cuáles son las técnicas o modelos más adecuados, resultando que frecuentemente son analizadas mediante estrategias que exigen ciertos supuestos matemáticos que las escalas de categorías no cumplen. Por este motivo, dentro de su simplicidad y sencillez son, no obstante, escalas con métrica delicada, lo que justifica las sugerencias analíticas que se han ido comentando.
Para este cometido, inicialmente expusimos algunos de los rasgos que caracterizan los análisis de estas escalas dentro del ámbito de las evaluaciones educativas. Después abordamos el confuso panorama de posturas y criterios existente, lo que puso de manifiesto la heterogeneidad de los enfoques y valoraciones de los distintos autores que han tratado este tema con anterioridad. Por esta razón hemos optado por recordar algunas técnicas estadística habituales, así como sugerir otras claramente novedosas -quizá por su complejidad- en el entorno de las evaluaciones educativas. En cualquier caso, todas ellas son sensibles a los supuestos matemáticos que exige el modelo que emplean y aseguran una correcta adaptación a la métrica de las escalas.
Un triple interés ha guiado nuestras aportaciones:
- Trabajar en torno a la medida de las escalas, bien a través de los cuantificadores lingüísticos de respuesta Likert, bien por medio de una transformación de escalas de frecuencia de respuestas con la ley de Zipf. Utilizando ambos procedimientos se consigue una mejora importante de la métrica de la escala, lo que permite emplear de forma correcta pruebas de mayor potencia, como test paramétricos, o el Análisis Factorial lineal.
- Sugerir análisis complementarios y sustitutivos del Análisis Factorial en su cometido de buscar dimensiones internas en los datos. Tal y como expusimos, la frecuencia del Análisis Factorial en estudios evaluativos, fundamentalmente de construcción de instrumentos, es incuestionable. Por ello nos ha parecido adecuado dedicar un espacio a aquellas alternativas del AF algo más complejas pero que, sin duda, se ajustan bien a este tipo de variables. Así se han comentado los desarrollos del AF en los entornos de los Modelos de Ecuaciones Estructurales y de la Teoría de Respuesta al Item (AF no lineal y AF de Información Completa).
- Demostrar la utilidad del Análisis Conjunto para llevar a cabo el estudio de respuestas no métricas efectuadas a partir de unas dimensiones establecidas previamente. En este sentido hemos valorado las diferencias entre ambos análisis, Factorial y Conjunto, y hemos justificado la conveniencia de éste último en aquellos estudios de evaluación de preferencias de una audiencia determinada.
Por último, se ha empleado la propuesta de evaluación de la Cohesión Social desde una perspectiva educativa de Jornet (2010), con el interés de ejemplificar de forma intuitiva y unificada las distintas sugerencias estadísticas expuestas anteriormente. Como resultado, los modelos sugeridos dan cuenta de sus posibilidades para analizar estructuras complejas que combinen planos, dimensiones, constructos, etc., atendiendo correctamente a la métrica delicada de las escalas que utilizan.
REFERENCIAS BIBLIOGRÁFICAS
Aizen, I. y Fishbein, M. (1980). Understanding Attitudes Predicting Social Behavior. New Jersey: Prentice Hall.
Akaah, I.P. y Korgaonkar, P.K. (1988) A conjoint investigation of the relative importance of risk relievers in direct marketing. Journal of Advertising Research, 28 (4), 38-44.
Bartholomew, D.J. (2007). Three faces of factor analysis. En R. Cudeck y R.C. MacCallum (Eds.), Factor analysis at 100. Historical development and future directions, pp. 9-21. Mahwah, NJ: LEA.
Bartholomew, D.J., Steele, F., Moustaki, I. y Galbrain, J.I. (2002). The analysis and interpretation of multivariate data for social scientists. Boca Raton, FL.: Chapman & Hall/CRC.
Bock, R.D., Gibbons, R. y Mulaki, E. (1988). Full-information item factor analysis. Applied Psychological Measurement, 12, 261-280.
Bock, R. D., Gibbons, R., Schilling, S. G., Muraki, E., Wilson, D. T. & Wood, R. (2003). TESTFACT 4.0. (Computer software and manual). Lincolnwood, IL: Scientific Software International.
Cañadas, I. y Sánchez-Bruno, A. (1998). Categorías de respuesta en escalas tipo Likert. Psicothema, 10 (3), 623-631.
Carifio, J. y Perla, R. (2007). Ten common misunderstandings, misconceptions, persistent myths and urban legends about Likert Scales and Likert response formats and their antidotes. Journal of Social Sciences, 2, 106-116.
Castelloe, J.M. (2000). Sample size computations and power analysis with the SAS System. Twenty-fifth Annnual Sas Users Group International Conference, Paper 265-25. Cary, NC: SAS Institute Inc.
Cattin, P., y D. R. Wittink (1982). Commercial use of conjoint analysis: a survey. Journal of Marketing, 46 (3) 44–53.
Cohen, J. (1962). The statistical power of abnormal social psychological research: a review. Journal of Abnormal and Social Psychology 65 (3), 145-153.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2ª ed.) Hillsdale, H.J.: LEA.
Consejo de Europa (2005). Elaboration concertée des indicateurs de la cohesión sociale. Guide méthodologique. Estrasburgo: Consejo de Europa.
Faraway, J.J. (2006). Extending the linear model with R. London: Chapman and Hall.
Ferrando, P.J. y Lorenzo, U. (1994). Recuperación de la solución factorial a partir de variables dicotomizadas. Psicothema, 6 (3), 483-491.
Fishbein, M. y Aizen, I. (1975). Belief, attitude, intention and behavior: an introduction to theory and research. Addison-Wesley.
Fraser, C. y McDonald, R. P. (1988). NOHARM II. Least-Squares item factor analysis. Multivariate Behavioral Research, 23, 267-269.
Gaviria, J.L. (1990). Factores de dificultad en el análisis de ítems. Qué son, por qué aparecen y posibles soluciones. Revista Complutense de Educación, 1 (1), 95-108.
Glass, G. V., Peckham, P. D. y Sanders, J. R. (1972). Consequences of failure to meet assumptions underlying the fixed analysis of variance and covariance. Review of Educational Research, 42, 237-288.
Green, P.E. y Rao, V.R. (1971). Conjoint measurement from quantifying judgmental data. Journal of Marketing Research, 8, 355-363.
Hair, J.F., Anderson, R.E., Tatham, R.L. y Black, W.C. (1999). Análisis multivariante (5ª ed.). Madrid: Prencice-Hall.
Hastie, T. y Tibshirani, R. (1990). Generalized additive models. London: Chapman and Hall.
Jamieson, S. (2004). Likert Scales: How to (ab)use them. Medical Education, 38 (12), 1212-1218.
Joaristi, L. y Lizasoain, L. (2008). Estudio de la dimensionalidad empleando análisis factorial clásico y análisis factorial de información total: análisis de pruebas de matemáticas de primaria (5º y 6º cursos) y secundaria obligatoria. RELIEVE, 14 (2) http://www.uv.es/RELIEVE/v14n2/RELIEVEv14n2_2.htm. Consultado en 10 de marzo de 2011.
Jöreskog, K.G. (2007). Factor analysis and its extensions. En R. Cudeck y R.C. MacCallum (Eds.), Factor analysis at 100. Historical development and future directions, pp. 47-77. Mahwah, NJ: LEA.
Jornet, J. (2010). Dimensiones docentes y cohesión social: reflexiones desde la evaluación. Ponecia presentada en el II Coloquio Red Iberoamericana de Investigadores sobre Evaluación de la Docencia. Valencia, septiembre 2010 (por cortesía del autor).
Likert, R. (1932). A technique for the measurement of attitudes. Archives of Psychology, 140, 55.
Likert, R. y Hayes, S. (1957). Some applications of behavioural research. Paris: Unesco.
López-González, E. (2003). Las pruebas de significación: una polémica abierta. Bordón. Revista de Pedagogía, 55 (2), 241-252.
López-González, E. y Hidalgo, R. (2010). Escalamiento Multidimensional No Métrico. Un ejemplo con R empleando el algoritmo SMACOF. ESE. Estudios sobre Educación, 18, 9-35.
López-González, E., Pérez-Carbonell, A. y Ramos, G. (2011). Modelos complementarios al Análisis Factorial en la construcción de escalas ordinales: un ejemplo aplicado a la medida del Clima Social Aula. Revista de Educación, 354, 369-397.
López González, E. y Ruiz-Soler, M. (2011). Análisis de datos con el Modelo Lineal Generalizado. Una aplicación con R. Revista Española de Pedagogía, 248, 59-80.
Lorenzo, U. y Ferrando, P.J. (2006). FACTOR: A computer program to fit the exploratory factor analysis model. Behavior Research Methods, 38, 88-91.
McDonald, R.D. (1967). Non linear factor analysis. Psychometric Monograph, 15.
Mulaki, E. y Carlson, J.E. (1995). Full-information factor analysis for polytomous item responses. Applied Psychological Measurement, 19, 73-90.
Mumby, P.J. (2002). Statistical power of non-parametric test: a quick guide for designing sampling strategies. Marine Pollution Bulletin, 44, 85-87.
Muthén, B. (1984). A general structural equation model with dichotomous, ordered, categorical and continuous latent variable indicators. Psychometrika, 49, 115-132.
Muthén, B. y Kaplan, D. (1992). A comparison of some methodologies for the factor analysis and non-normal Likert variables: a note on de size of the models. British Journal of the Mathematical and Statistical Psychology, 45, 19-30.
Noether, G. E. (1987). Sample size determination for some common nonparametric tests. Journal of the American Statistical Association, 82, 645-647.
O’Brien, R.G. (1998). A tour of UnifyPow: a SAS module/macro for sample-size analysis. Twenty-third Annual SAS Users Group International Conference. Cary, NC: SAS Institute Inc.
Özmen, I, Yaşıt, B. y Sezgin, O (2006). A Conjoint Analysis to Determine the Preferences for Some Selected MBA Programs. RELIEVE, 12 (1). http://www.uv.es/RELIEVE/v12n1/RELIEVEv12n1_7.htm. Consultado en 10 de marzo de 2011.
Raudenbush, S.W. y Bryk, A.S. (2002). Hierarchical linear models (2ª ed). London: Sage.
Ruiz Soler, M. (2004). Aplicación de la Ley de Zipf en la investigación psicológica. Metodología de las Ciencias del Comportamiento, Volumen Especial, 715-722.
Ruiz-Soler, M. y López-González, E. (2009). El entorno estadístico R: ventajas de su uso en la docencia y la investigación. Revista Española de Pedagogía, 243, 255-274.
SAS Institute Inc. (2008). User’s guide introduction to power and simple analysis (Book excerpt). En SAS Institute Inc. User’s Guide 9.2. Cary, NC: SAS Institute Inc.
Siegel, S. (1988) Estadística no paramétrica aplicada a las ciencias de la conducta (2ª ed.). México: Trillas.
Schriesheim, C. y Castro, S. (1996). Referent effects in the magnitude estimation scaling of frequency expressions for response anchor sets: an empirical investigation. Educational and Psychological Measurement, 56, 557-569.
Suárez, J. y Jornet, J. (2011). Las competencias y el uso de las Tecnologías de Información y Comunicación (TIC) por el profesorado: estructura dimensional. Revista Electrónica de Investigación Educativa (en prensa, por cortesía de los autores).
Swygert, K.A., McLeod, L.D. y Thissen, D. (2001). Factor analysis for items or testlets in more than two categories. En D. Thissen y H. Wainer (Eds.), Test Scoring, pp. 217-250. Mahwah, NJ: LEA.
Varela, J., Rial, A. y García-Carreira, A. (2003). Análisis conjunto. En J.P. Levy y J. Varela (dirs): Análisis multivariable para las Ciencias Sociales, pp. 507-566. Madrid: Prentice-Hall.
Wood, S.N. (2006). Generalized additive models: an introduction with R. London:Chapman and Hall.
Yela, M. (1996). Los test y el análisis factorial. Psicothema, 8 (1), 73-88.
Zipf, G. (1949). Human Behavior and the Principle of Least Efford. Reading, MA: Addison-Wesley.
{1} En el presente trabajo se utiliza el término escala de categorías con un doble sentido: como instrumento constituido por varios ítems, elementos o reactivos, todos ellos midiendo un mismo constructo, y como nivel de medida no métrica, categórica (discreta, nominal u ordinal) de un sencillo ítem, reactivo o variable. La distinción entre un sentido u otro es importante, pero en el caso que aquí nos ocupa (el uso de modelos estadísticos adecuados), las escalas de categorías (instrumentos) constituyen también variables con niveles de medida no métrica, por tanto, con métrica delicada.
{2} El programa PASS (Power Analysis and Sample Size) realiza análisis de la potencia para pruebas no paramétricas (ver http://www.ncss.com/pass.html). La oferta más completa para distintos modelos se encuentra en el software SAS (Statistical Analysis System), incluyendo también técnicas para calcular la potencia en pruebas no paramétricas (O’Brien, 1998; Castelloe, 2000 y SAS, 2008).
{3} Según las conclusiones recogidas en el trascendente estudio Montecarlo de Glass et al. (1972), la prueba F es increíblemente robusta a la violación de la condición de datos de intervalo, siempre que se trabaje con una escala o subescala de 4 a 8 items y utilizando de 5 a 7 puntos de formato de respuesta Likert.
{4} Como hemos indicado, el uso del AC en el entorno educativo es francamente escaso. No obstante, una aplicación en este ámbito puede consultarse en Özmen y Sezgin (2006)
{5} El Consejo de Europa define la Cohesión Social de una sociedad moderna como la capacidad de la sociedad para garantizar la sostenibilidad del bienestar de todos sus miembros, incluido el acceso equitativo a los recursos disponibles, la dignidad en la diversidad y la autonomía personal y colectiva, y a la participación responsable (Consejo de Europa, 2005: 23 –tomado de Jornet, 2010-).
{6}Proyecto AVACO: Análisis de Variables de Contexto: Diseño de cuestionarios de Contexto para la Evaluación de Sistemas Educativos (SEJ 2005-05995, financiado por el Ministerio de Educación y Ciencia, España) y proyecto MAVACO: Modelos de Análisis de Variables de Contexto para la Evaluación de Sistemas Educativos (EDU 2009-13485, financiado por el Ministerio de Ciencia e Innovación, España).
{7} La valoración de estos modelos excede a los objetivos asumibles en el presente trabajo. No obstante constituyen una muy interesante estrategia para analizar relaciones de dependencia no lineales. El lector interesado puede consultar Faraway (2006), con un nivel más sencillo, y Hastie y Tibshirani (1990) y Wood (2006), más avanzado. Estos autores han diseñado los dos paquetes que trabajan los modelos aditivos en el programa R: gam por Hastie y Tibshirani y mgcv por Wood.
{8} Las recomendaciones acerca del tamaño muestral para un AC han ido variando. Cattin y Wittink, en un análisis de (1982), vieron que solía variar entre 100 a 1000 sujetos, siendo lo más habitual de 300 a 500. En otro estudio posterior, Akaah y Korgaonkar (1988) observaron que se trabajaba con tamaños menores, incluso menos de 100 casos.